WBBSE Class 9 বহুপদী সংখ্যামালা Koshe Dekhi 7.4 সমাধান

WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪ | গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান | WBBSE Gonit Prokash Class 9 Math Chapter 7 Koshe dekhi 7.4 Polynomial Solution.

WBBSE Class 9 Koshe Dekhi 7.4 Solution | নবম শ্রেণি কষে দেখি ৭.৪ সমাধান

Ex 1. নীচের বহুপদী সংখ্যামালাগুলির মধ্যে কোনগুলির একটি উৎপাদক (x+1) হিসেব করে লিখি।

(i) 2x³+3x²-1

(ii) x⁴+ x³-x²+4x+5

(iii) 7x³+x²+7x+1

(iv) 3+3x-5x³-5x⁴

(v) x⁴+x²+x+1

(vi) x³+x²+x+1

সমাধান:

1.(i) ধরি, f(x) = 2x³+3x²-1

x+1 = 0 ⇒ x = -1

সুতরাং (x+1) বহুপদী সংখ্যামালার শূন্য -1

এখন f(-1) = 2(-1)³+3(-1)²-1 = -2+3-1= 0

∴ f(-1)=0 ⇒ গুণনীয়ক উপপাদ্য অনুসারে, f(x) বহুপদী সংখ্যামালার একটি উৎপাদক হল (x+1).

1.(ii) ধরি, f(x) = x⁴+x³-x²+4x+5

x+1= 0 

বা, x = -1

∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1

এখন f(-1) = (-1)⁴+(-1)³-(-1)²+4(-1)+5

               = 1-1-1-4+5

               = 0

যেহেতু f(-1)=0, তাই গুণনীয়ক উপপাদ্য অনুযায়ী (x+1) হল f(x) বহুপদী সংখ্যামালার একটি উৎপাদক।

 

 

1.(v) ধরি, f(x)= x⁴+x²+x+1

x+1=0   ⇒ x = -1

∴ (x+1) বহুপদী সংখ্যামালার শূন্য  -1

এখন f(-1) = (-1)⁴+(-1)²+(-1)+1

                = 1+1-1+1

                = 2 ≠ 0

যেহেতু f(-1) ≠ 0, তাই গুণনীয়ক উপপাদ্য অনুযায়ী (x+1), f(x)=x⁴+x²+x+1 বহুপদী সংখ্যামালার উৎপাদক নয়।

1.(vi) ধরি, f(x) = x³+x²+x+1

x+1=0 

⇒ x = -1

⇒ (x+1) বহুপদী সংখ্যামালার শূন্য  -1

এখন f(-1) = (-1)³+(-1)²+(-1)+1

               = -1+1-1+1 = 0

যেহেতু f(-1) = 0, তাই গুণনীয়ক উপপাদ্য অনুসারে (x+1) হল f(x)= x³+x²+x+1 বহুপদী সংখ্যামালার একটি উৎপাদক।

 

Ex 2. গুণনীয়ক উপপাদ্য ব্যবহার করে নীচের বহুপদী সংখ্যামালাগুলি f(x)-এর একটি উৎপাদক g(x) কিনা লিখি ।

(i) f(x) = x⁴-x²-12 এবং g(x) = x+2

(ii) f(x) = 2x³+9x²-11x-30 এবং g(x) = x+5

(iii) f(x) = 2x³ +7x² -24x -45 এবং g(x) = x-3

(iv) f(x) = 3x³+x²-20x +12 এবং g(x) = 3x-2

সমাধান:

2.(i) g(x) = x+2 বহুপদী সংখ্যামালার শূন্য পাই নিচের সমীকরণটি সমাধান করে।

x+2 =0

⇒ x = -2

⇒ g(x) বহুপদী সংখ্যামালার শূন্য -2 ।

এখন f(x) = x⁴-x²-12

∴ f(-2) = (-2)⁴ -(-2)² -12

          =16 – 4-12

          =16-16 = 0

এতএব f(-2) = 0. তাই গুণনীয়ক উপপাদ্য অনুসারে f(x) এর একটি উৎপাদক হল g(x) 

2.(ii) g(x) = x+5 বহুপদী সংখ্যামালার শূন্য পাই নিচের সমীকরণটি সমাধান করে।

x+5 =0   ⇒ x = -5

⇒ g(x) বহুপদী সংখ্যামালার শূন্য -5 

এখন f(x) =2x³+9x²-11x-30

∴ f(-5) = 2(-5)³ +9(-5)² -11(-5) -30

          = 2 (-125) +9(25) +55 – 30

          = -250+225+55-30 =0

এতএব f(-5) = 0. তাই গুণনীয়ক উপপাদ্য অনুযায়ী f(x) এর একটি উৎপাদক হল g(x) 

 

 

 

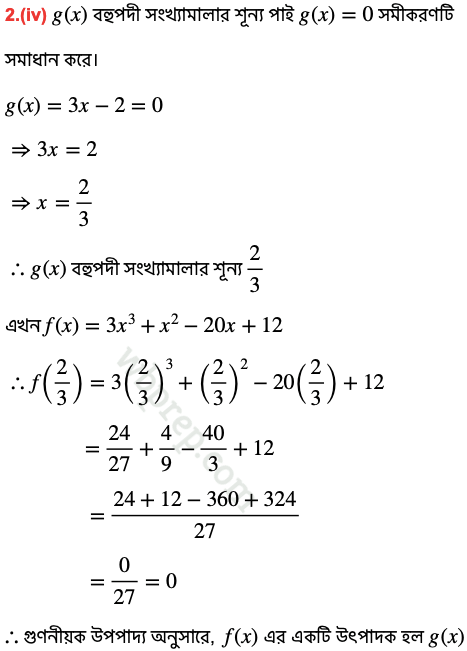
Ex 3. k-এর মান কত হলে x+2 দ্বারা 2x⁴+3x³+2kx²+3x+6 বহুপদী সংখ্যামালাটি বিভাজ্য হবে হিসাব করে লিখি।

সমাধান:

ধরি, f(x) = 2x⁴+3x³+2kx²+3x+6  এবং g(x) = x+2

g(x)=0  ⇒ x+2 =0  ⇒ x = -2

∴ g(x) বহুপদী সংখ্যামালার শূন্য -2

যেহেতু f(x) বহুপদী সংখ্যামালাটি g(x) দ্বারা বিভাজ্য, গুণনীয়ক উপপাদ্য অনুসারে আমরা পাই

f(-2) = 0

⇒ 2(-2)⁴+3(-2)³+2k(-2)²+3(-2)+6 =0

⇒ 32 -24 +8k -6+6 = 0

⇒ 8k +8 = 0

⇒ k = -8/8 = -1

∴ k = -1 হলে f(x) বহুপদী সংখ্যামালাটি g(x) দ্বারা বিভাজ্য হবে।

 

Ex 4. k-এর মান কত হলে নীচের বহুপদী সংখ্যামালাগুলি f(x) -এর একটি উৎপাদক g(x) হবে হিসেব করি-

(i) f(x) = 2x³+9x²+x+k এবং g(x) = x-1

(ii) f(x)= kx²-3x+k এবং g(x) = x-1

(iii) f(x) = 2x⁴+x³-kx²-x+6 এবং g(x) = 2x-3

(iv) f(x) = 2x³+kx²+11x+k+3 এবং g(x) = 2x-1

সমাধান:

4.(i) g(x) = x-1 বহুপদী সংখ্যামালার শূন্য পাই নিচের সমীকরণটি সমাধান করে।

x-1 =0   ⇒ x = 1

∴ g(x) = x-1 বহুপদী সংখ্যামালার শূন্য 1 

এখন f(x) = 2x³+9x²+x+k. যেহেতু f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x), তাই গুণনীয়ক উপপাদ্য অনুসারে আমরা পাই

f(1) = 0 

⇒ 2⋅1³ +9⋅1²+1+k =0

⇒ 2+9+1+k = 0

⇒ k = -2-9-1 = -12

∴ k = -12 হলে f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x) হবে।

4.(ii) g(x) = x-1 বহুপদী সংখ্যামালার শূন্য পাই x-1=0 সমীকরণটি সমাধান করে।

x-1 =0   ⇒ x = 1

∴ g(x) = x-1 বহুপদী সংখ্যামালার শূন্য 1 

এখন f(x) = kx² -3x+k. যেহেতু f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x), তাই গুণনীয়ক উপপাদ্য অনুযায়ী আমরা পাই

f(1) = 0 

⇒ k⋅1³ -3⋅1+k =0

⇒ k -3+k = 0

⇒ 2k = 3

⇒ k = $\frac{3}{2}$

∴ k = $\frac{3}{2}$ হলে f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x) হবে।

 

Ex 5. ax⁴+2x³-3x²+bx-4 বহুপদী সংখ্যামালার উৎপাদক x²-4 হলে a ও b এর মান কত হবে হিসেব করে লিখি।

সমাধান:

x²-4=0   ⇒ x= ±2

∴ x²-4 বহুপদী সংখ্যামালার শূন্য ±2

ধরি, f(x) = ax⁴+2x³-3x²+bx-4.

যদি x²-4, f(x)-এর উৎপাদক হয় তাহলে গুণনীয়ক উপপাদ্য অনুসারে f(±2)=0.

এখন f(2)=0

⇒ a⋅2⁴ +2⋅2³ -3⋅2² +b⋅2 -4 = 0

⇒ 16a +16 -12 +2b -4 =0

⇒ 16a+2b = 0

⇒ 8a+b = 0 …(i)

আবার f(-2)=0

⇒ a(-2)⁴+2(-2)³-3(-2)²+b(-2) -4 = 0

⇒ 16a -16 -12 -2b -4 =0

⇒ 16a-2b = 32

⇒ 8a – b = 16 …(ii)

(i)+(ii) করে পাই, 16a=16 ⇒ a=1.

∴ সমীকরণ (ii) থেকে পাই, 

8⋅1 -b=16 

⇒ b = 8-16 = -8

সুতরাং a = 1 এবং b = -8.

 

Ex 6. x³ +3x²+2ax+b বহুপদী সংখ্যামালার দুটি উৎপাদক (x+1) ও (x+2) হলে, a ও b এর মান কত হবে হিসাব করে লিখি।

সমাধান:

x+1 =0   ⇒ x = -1

∴ x+1 বহুপদী সংখ্যামালার শূন্য -1 

x+2 =0   ⇒ x = -2

∴ x+2 বহুপদী সংখ্যামালার শূন্য -2

ধরি, f(x) = x³ +3x²+2ax+b

যেহেতু x+1 এবং x+2 উভয়ই f(x)-এর উৎপাদক, তাই গুণনীয়ক উপপাদ্য অনুসারে আমরা পাই

f(-1)=0 এবং f(-2)=0.

এখন f(-1)=0

⇒ (-1)³+3(-1)²+2a(-1) +b = 0

⇒ -1+3 -2a +b = 0

⇒ -2a+b = -2

⇒ 2a-b = 2 …(i)

আবার f(-2)=0

⇒ (-2)³+3(-2)²+2a(-2) +b = 0

⇒ -8+12 -4a +b = 0

⇒ 4a-b = 4 …(ii)

(ii)-(i) করে পাই, 4a-b – (2a-b) = 4-2

⇒ 2a = 2 

⇒ a = 1

∴ সমীকরণ (ii) থেকে পাই, 

4⋅1 -b = 4

⇒ 4-b = 4 

⇒ b = 0 

সুতরাং a = 1 এবং b = 0.

 

Ex 7. ax³+bx²+x-6 বহুপদী সংখ্যামালাকে (x-2) দ্বারা ভাগ করলে ভাগশেষ 4 হয় এবং এই বহুপদী সংখ্যামালার একটি উৎপাদক x+2 হলে a ও b-এর মান কত হবে হিসাব করি।

সমাধান:

ধরি, f(x) = ax³+bx²+x-6

x-2 = 0  ⇒ x =2

∴ (x-2) বহুপদী সংখ্যামালার শূন্য 2 

যেহেতু f(x) বহুপদী সংখ্যামালাকে (x-2) দ্বারা ভাগ করলে ভাগশেষ হয় 4, তাই ভাগশেষ উপপাদ্য অনুসারে আমরা পাই

f(2) = 4

⇒ a⋅2³ +b⋅2² +2 -6 = 4

⇒ 8a+4b -4 = 4

⇒ 8a +4b = 8

⇒ 2a +b = 2 …(i)

অন্যদিকে, f(x) বহুপদী সংখ্যামালার একটি উৎপাদক x+2

x+2 = 0  ⇒ x = -2

∴ x+2 বহুপদী সংখ্যামালার শূন্য -2 । যেহেতু f(x) বহুপদী সংখ্যামালার একটি উৎপাদক x+2, সুতরাং গুণনীয়ক উপপাদ্য অনুসারে আমরা পাই

f(-2) = 0 

⇒ a(-2)³+b(-2)²+(-2) -6 = 0

⇒ -8a+4b -8 = 0

⇒ 8a-4b = -8

⇒ 2a-b = -2 …(ii)

(i)+(ii) করে পাই, 4a=0 ⇒ a=0.

∴ সমীকরণ (ii) থেকে পাই, 

2⋅0 -b= -2 

⇒ b = 0+2 = 2

সুতরাং a = 0 এবং b = 2.

 

Ex 8. n যেকোনো ধনাত্মক পূর্ণসংখ্যা (যুগ্ম বা অযুগ্ম) হলে দেখাই যে xⁿ –yⁿ বহুপদী সংখ্যামালাটির একটি উৎপাদক x-y.

সমাধান:

Ex 9. n যেকোনো অযুগ্ম ধনাত্মক পূর্ণসংখ্যা হলে দেখাই যে xⁿ +yⁿ বহুপদী সংখ্যামালাটির একটি উৎপাদক x+y.

সমাধান:

Ex 10. n যেকোনো ধনাত্মক পূর্ণসংখ্যা (যুগ্ম বা অযুগ্ম) হলে দেখাই যে xⁿ +yⁿ বহুপদী সংখ্যামালাটির একটি উৎপাদক কখনই x-y হবে না।

সমাধান:

 

Ex 11. বহু বিকল্পীয় প্রশ্ন: (M.C.Q)

11.(i) x³+6x²+4x+k বহুপদী সংখ্যামালাটি (x+2) দ্বারা বিভাজ্য হলে k এর মান-

(a) -6

(b) -7

(c ) -8

(d) -10

Answer: (c) -8

সমাধান: 

x+2=0   ⇒ x= -2.

∴ x+2 বহুপদী সংখ্যামালার শূন্য -2

ধরি, f(x) =x³+6x²+4x+k । যেহেতু f(x) বহুপদী সংখ্যামালা (x+2) দ্বারা বিভাজ্য, তাই f(x)-কে (x+2) দ্বারা ভাগ করলে ভাগশেষ হবে 0 । সুতরাং ভাগশেষ উপপাদ্য অনুযায়ী আমরা পাই

f(-2) = 0

⇒ (-2)³+6(-2)² +4(-2) + k = 0

⇒ -8 +24 -8 +k = 0

⇒ 8+k = 0

⇒ k = -8

11.(ii) f(x) বহুপদী সংখ্যামালার $f(-\frac{1}{2}) = 0$ হলে $f(x)$ এর একটি উৎপাদক হবে

(a) 2x-1

(b) 2x+1

(c) x-1

(d) x+1

Answer: (b) 2x+1

সমাধান: 

যেহেতু f(-1/2) =0, তাই আমরা পাই

x= -1/2

⇒ 2x= -1

⇒ 2x+1 =0

∴ f(x) –এর একটি উৎপাদক হল 2x+1.

11.(iii) f(x) বহুপদী সংখ্যামালার (x-1) একটি উৎপাদক কিন্তু g(x) বহুপদী সংখ্যামালার উৎপাদক নয়। সুতরাং (x-1) একটি উৎপাদক হবে

(a) f(x) g(x)

(b) -f(x) +g(x)

(c) f(x) – g(x)

(d) {f(x)+ g(x)} g(x)

Answer: (a) f(x) g(x)

সমাধান: 

যেহেতু f(x) =0 বহুপদী সংখ্যামালার একটি উৎপাদক x-1, তাই (x-1) হল { f(x) × অন্য যেকোনো বহুপদী সংখ্যামালা} -র একটি উৎপাদক। তাই সঠিক উত্তরটি হল (a) f(x) g(x).

11.(iv) xⁿ+1 বহুপদী সংখ্যামালার (x+1) একটি উৎপাদক হবে যখন

(a) n একটি অযুগ্ম ধনাত্মক পূর্ণ সংখ্যা

(b) n একটি যুগ্ম ধনাত্মক পূর্ণসংখ্যা

(c) n একটি ঋনাত্মক পূর্ণসংখ্যা

(d) n একটি ধনাত্মক পূর্ণ সংখ্যা

Answer: (a) n একটি অযুগ্ম ধনাত্মক পূর্ণ সংখ্যা

সমাধান: 

x+1=0   ⇒ x= -1

∴ x+2 বহুপদী সংখ্যামালার শূন্য -1

ধরি, f(x) = xⁿ+1. যদি (x+1), f(x)-এর উৎপাদক হয় তাহলে f(-1)=0.

∴ (-1)ⁿ+1=0

⇒ (-1)ⁿ =-1. এটি তখনই সম্ভব যখন n একটি অযুগ্ম ধনাত্মক পূর্ণ সংখ্যা।

11.(v) an⁴+bn³+cn²+dn+e বহুপদী সংখ্যামালার n²-1 উৎপাদক হলে

(a) a+c+e=b+d

(b) a+b+e=c+d

(c) a+b+c=d+e

(d) b+c+d=a+e

Answer: (a) a+c+e=b+d.

সমাধান: 

n²-1=0   ⇒ n= ±1

∴ n²-1 বহুপদী সংখ্যামালার শূন্য ±1

ধরি, f(n) = xⁿ+1. যদি n²-1, f(n)-এর উৎপাদক হয় তাহলে গুণনীয়ক উপপাদ্য অনুসারে f(±1)=0.

এখন f(1)=0

⇒ a⋅1⁴+b⋅1³+c⋅1²+d⋅1+e =0

⇒ a+b+c+d+e =0

অন্যদিকে f(-1)=0

⇒ a⋅(-1)⁴+b⋅(-1)³+c⋅(-1)²+d⋅(-1)+e =0

⇒ a-b+c-d+e =0

⇒ a+c+e = b+d

∴ option (a) সঠিক।

 

Ex 12. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন:

12.(i) x³+ax² -2x+a-12 বহুপদী সংখ্যামালার x+a একটি উৎপাদক হলে a -এর মান কত হিসাব করে লিখি।

সমাধান:

x+a = 0 ⇒ x = -a

∴ (x+a) বহুপদী সংখ্যামালার শূন্য -a

ধরি, f(x) = x³+ax²-2x+a-12

যেহেতু (x+a) , f(x)-এর একটি উৎপাদক গুণনীয়ক উপপাদ্য অনুযায়ী আমরা পাই

f(-a) = 0 

⇒ (-a)³ +a(-a)²-2(-a)+a -12 =0

⇒ -a³+a³+2a+a-12 =0

⇒ 3a = 12

⇒ a = 4

∴ a এর মান হল 4 

12.(ii) k²x³-kx² +3kx – k বহুপদী সংখ্যামালার x-3 একটি উৎপাদক হলে k-এর মান কত হিসাব করে লিখি।

সমাধান:

x-3 = 0 ⇒ x = 3

∴ x-3 বহুপদী সংখ্যামালার শূন্য 3

ধরি, f(x) = k²x³-kx² +3kx – k

যেহেতু (x-3) , f(x)-এর একটি উৎপাদক গুণনীয়ক উপপাদ্য অনুসারে আমরা পাই

f(3) = 0 

⇒ k²⋅3³ – k⋅3² +3k⋅3 -k =0

⇒ 27k² – 9k +9k -k =0

⇒ 27k² -k =0

⇒ k(27k -1) =0

হয় k=0  অথবা 27k-1 = 0

                    ⇒ k = 1/27.

∴ k-এর মান হল 0 অথবা 1/ 27

12.(iii) f(x) =2x+5 হলে f(x) +f(-x) -এর মান কত হবে লিখি।

সমাধান:

f(x) = 2x+5

∴ f(x)+f(-x) = {2x+5} + {2(-x)+5}

= 2x+5-2x+5

= 10

12.(iv) px²+5x+r বহুপদী সংখ্যামালার (x -2) এবং (x-$\frac{1}{2}$) উভয়ই উৎপাদক হলে p ও r-এর মধ্যে সম্পর্ক হিসাব করে লিখি।

সমাধান:

x-2 = 0 ⇒ x = 2

∴ (x-2) বহুপদী সংখ্যামালার শূন্য 2

আবার x $-\frac{1}{2}$ = 0 ⇒ x = $\frac{1}{2}$

∴ (x$-\frac{1}{2}$)বহুপদী সংখ্যামালার শূন্য $\frac{1}{2}$.

ধরি, f(x) = px²+5x+r

যদি x-2 এবং (x-$\frac{1}{2}$) উভয়ই f(x)-এর উৎপাদক হয় তাহলে গুণনীয়ক উপপাদ্য অনুসারে আমরা পাই

f(2)=0 এবং f($\frac{1}{2}$)=0.

এখন f(2)=0

⇒ p⋅2²+5⋅2+r = 0

⇒ 4p +10 +r = 0

⇒ 4p+r = -10 …(i)

আবার $f(\frac{1}{2})$ = 0

⇒ $p \cdot (\frac{1}{2})^2+ 5 \cdot \frac{1}{2}+r = 0$

⇒ $\frac{p}{4}+ \frac{5}{2}+r =0$

⇒ $\frac{p+10+4r}{4}=0$

⇒ p+10+4r = 0

⇒ p+4r = -10 …(ii)

(i) নং ও (ii) নং সমীকরণ থেকে পাই ,

4p+r =p+4r

⇒ 4p-p = 4r-r

⇒ 3p = 3r

⇒ p  = r

∴ p ও r এর মধ্যে নির্ণেয় সম্পর্ক হল p = r.

12.(v) f(x) =2x+3 রৈখিক বহুপদী সংখ্যামালার বীজ কত হবে লিখি।

সমাধান:

f(x) =2x+3 রৈখিক বহুপদী সংখ্যামালার বীজ পাওয়া যায় f(x) = 0 সমীকরণটি সমাধান করে।

f(x) = 0 ⇒ 2x+3 = 0

⇒ 2x = -3

⇒ x = $-\frac{3}{2}$

∴ f(x) =2x+3 রৈখিক বহুপদী সংখ্যামালার বীজ $-\frac{3}{2}$.