[লগারিদম] WBBSE Class 9 Koshe Dekhi 21 Solutions

Koshe Dekhi 21 Class 9 | Class 9 Logarithm Koshe Dekhi 21 Solutions | গণিত প্রকাশ ক্লাস ৯ লগারিদম কষে দেখি ২১ সমাধান | WBBSE Class 9 Logarithm Chapter 7 Solution | লগারিদম কষে দেখি ২১ সমাধান  | Ganit Prakash Class 9 Solution Koshe Dekhi 21 | Solution of WB Board Class 9 Logarithm Exercise 21 |  গণিত প্রকাশ নবম শ্রেণি কষে দেখি ২১ সমাধান

WBBSE Class 9 Math Koshe Dekhi 21 Solutions | গণিত প্রকাশ নবম শ্রেণি কষে দেখি ২১ সমাধান

WBBSE Class 9 Logarithm Koshe Dekhi 21 Question 1 Solution

Ex 1. মান নির্ণয় করি

WBBSE Class 9 Logarithm Question 2 Solution:

Ex 2.(a) 625 এর লগারিদম 4 হলে, নিধান কী হবে হিসাব করে লিখি।

সমাধান:

ধরি, নিধান x । শর্তানুসারে আমরা পাই

 log_x 625 = 4

⇒ x⁴ = 625  [∵ log_ab=x ⇒ a^x=b ]

⇒ x⁴ = 5⁴

⇒ x = 5

সুতরাং নিধান 5 

Ex 2.(b) 5832 -এর লগারিদম 6 হলে, নিধান কী  হবে হিসাব করে লিখি।

সমাধান:

ধরি, নিধান x । শর্তানুসারে, আমরা পাই

 log_x 5832 = 6

⇒ x⁶ = 5832  [∵ log_ab=x ⇒ a^x=b ]

⇒ x⁶ = 2³×3⁶

⇒ x⁶ = (√2)⁶×3⁶ [∵ √2=2^1/2 ]

⇒ x⁶ = (3√2)⁶

⇒ x = 3√2

∴ নির্ণেয় নিধান 3√2

WBBSE Class 9 Logarithm Koshe Dekhi 21 Question 3 Solution

Ex 3.(a) 1+log₁₀a = 2 log₁₀b হলে a কে b দ্বারা প্রকাশ করি।

সমাধান:

1+log₁₀a = 2 log₁₀b

⇒ log₁₀10 +log₁₀a = log₁₀b²  [∵ log_aa=1 এবং n log_ab = log_abⁿ ]

⇒ log₁₀10a = log₁₀b²  [∵ log_aM + log_aN = log_aMN ]

লগারিদমের নিধান সমান হওয়াই আমরা পাই,

10a = b²

⇒ a = $\frac{b^2}{10}$

∴ a কে b দ্বারা প্রকাশ করা গেল।

Ex 3.(b) 3+log₁₀x = 2 log₁₀y হলে x কে y -এর দ্বারা প্রকাশ করি।

সমাধান:

3+log₁₀x = 2 log₁₀y

⇒ log₁₀10³ +log₁₀x = log₁₀y²  [∵ log_aa^k =k এবং n log_ab = log_abⁿ ]

⇒ log₁₀(10³x) = log₁₀y²  [∵ log_aM + log_aN = log_aMN ]

লগারিদমের নিধান সমান হওয়াই আমরা পাই,

10³x = y²

⇒ 1000x = y²

⇒ $x = \frac{y^2}{1000}$

∴ x কে y –এর দ্বারা প্রকাশ করা গেল।

ক্লাস ৯ লগারিদম কষে দেখি ২১ Question 4 Solution

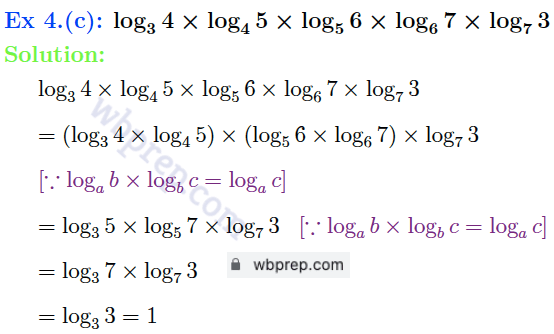
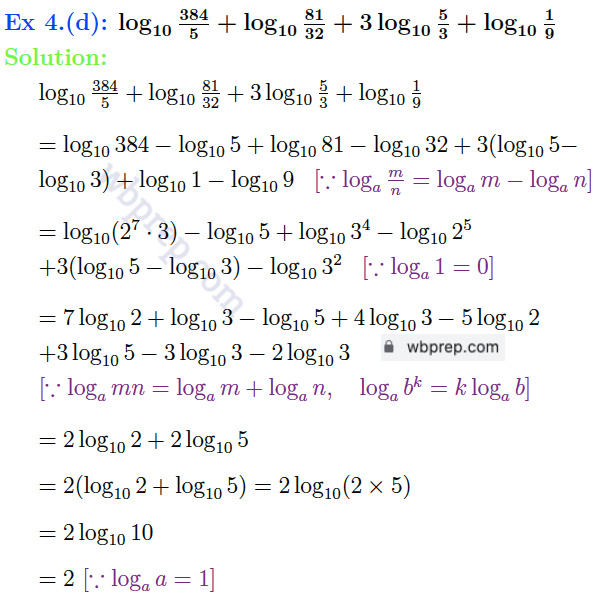
গণিত প্রকাশ ক্লাস ৯ লগারিদম কষে দেখি ২১ Question 5 সমাধান

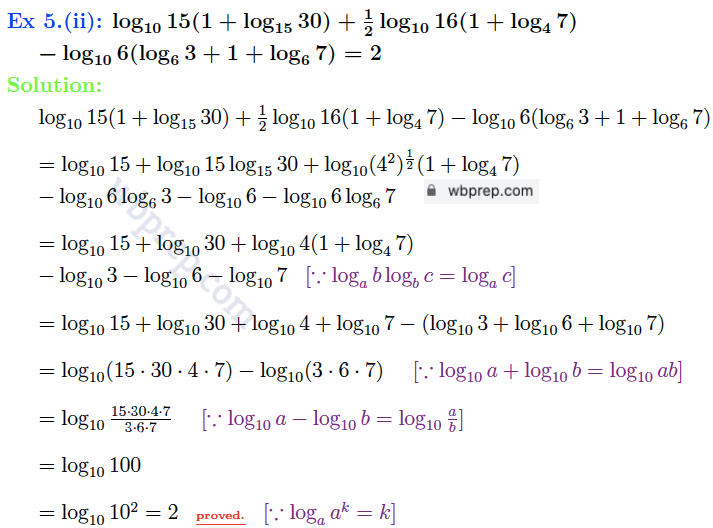
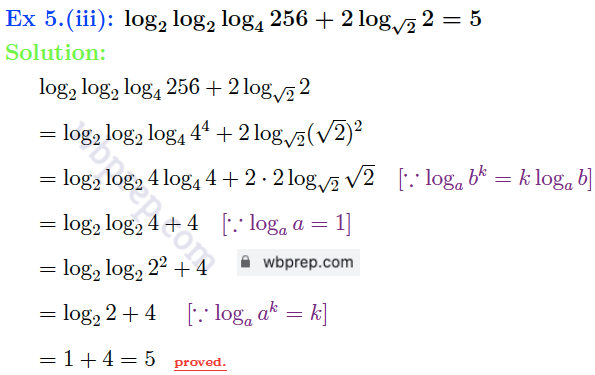
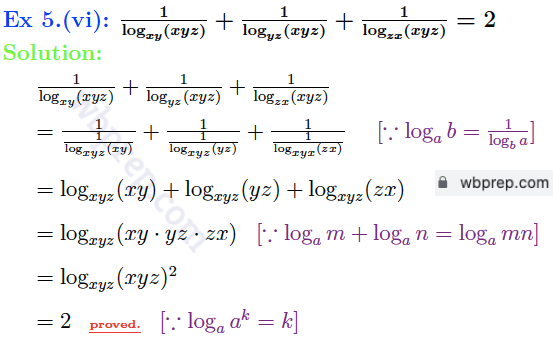
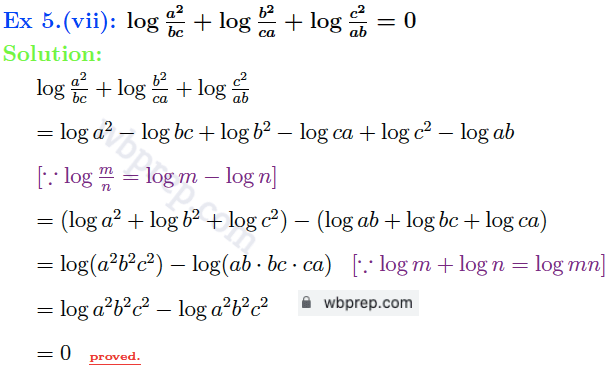
গণিত প্রকাশ ক্লাস ৯ লগারিদম কষে দেখি ২১ Question 6 সমাধান

Ex 6.(i) যদি log (x+y)/5=1/2(log x+log y) হয়, তাহলে দেখাই যে x/y+y/x=23

সমাধান:

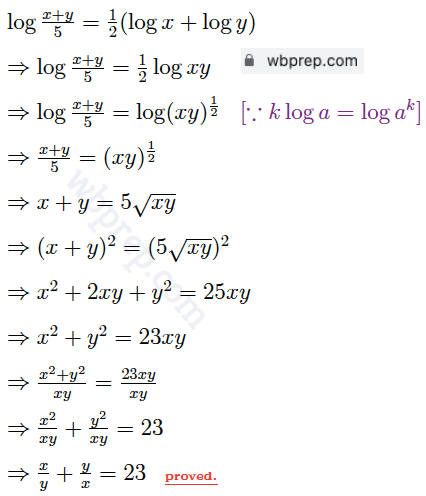
Ex 6.(ii) যদি a⁴+b⁴ = 14a²b² হয়, তাহলে দেখাই যে, log(a²+b²) =log a +log b+2log 2

সমাধান:

a⁴+b⁴ = 14a²b²

⇒ (a²)² + (b²)² = 14a²b²

⇒ (a²+b²)² -2a²b² = 14a²b²

⇒ (a²+b²)² = 16a²b²

⇒ (a²+b²)² =  (4ab)²

উভয়পক্ষে বর্গমূল নিয়ে পাই,

 (a²+b²) = 4ab

উভয়পক্ষে log নিয়ে পাই,

log(a²+b²) = log (4ab)

= log 4+loga+log b

=log 2² +log a +log b

=2log 2 +log a +log b

=log a +log b+2log 2  proved

Ganit Prakash Koshe Dekhi 21 Question 7 Solution

ক্লাস ৯ লগারিদম কষে দেখি ২১ Question 8 সমাধান

ক্লাস ৯ লগারিদম কষে দেখি ২১ Question 9 সমাধান

Ex 9. যদি, a ^3-x . b^5x = a^5+x . b^3x হয়, তাহলে দেখাই যে , x log (b/a)= loga

সমাধান:

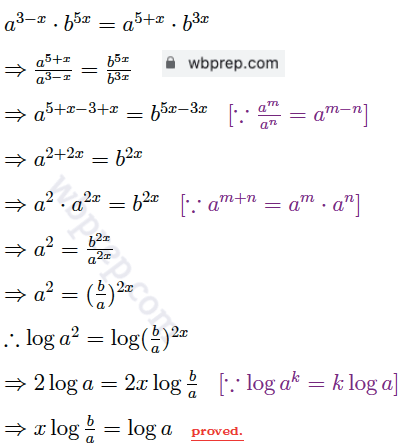
গণিত প্রকাশ লগারিদম কষে দেখি ২১ Question 10 সমাধান

Ex 10. সমাধান করি: 

Ex 10(a). Solve log₈ [log₂{log₃ (4^x+17)}] = 1/3

সমাধান:

log₈ [log₂{log₃ (4^x+17)}] = 1/3

⇒  log₂{log₃(4^x+17)} = 8^1/3

⇒  log₂{log₃(4^x+17)} = 2^3×1/3

⇒  log₂{log₃(4^x+17)} = 2

⇒  log₃(4^x+17) =2²

⇒ log₃(4^x+17) = 4

⇒ 4^x+17 = 3⁴

⇒ 4^x+17 = 81

⇒ 4^x= 81-17

⇒ 4^x = 64 = 4³

⇒ x = 3

লগারিদম কষে দেখি ২১ Question 11 সমাধান

Ex 11. দেখাই log₁₀2 -এর মান 1/4 এবং 1/3 এর মধ্যে অবস্থিত।

সমাধান:

ধরি,  log₁₀2 = x

∴ 10^x = 2  ⇒10^12x = 2¹² = 4096

যেহেতু 1000 < 4096  < 10000, তাই আমরা পাই

10³ < 2¹² < 10⁴

⇒ 10³ < 10^12x < 10⁴

⇒ 3 < 12x < 4

⇒ 3/12 < x < 4/12

⇒ 1/4 < x < 1/3 

সুতরাং log₁₀2 -এর মান 1/4 এবং 1/3 এর মধ্যে অবস্থিত  proved

Ex 12. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)

Ex 12.(i) যদি log_√x 0.25 = 4 হয়, তাহলে x -এর মান

(a) 0.5   (b) 0.25   (c) 4  (d) 16

সঠিক উত্তরটি হলো (a) 0.5

সমাধান:

log_√x 0.25 = 4

⇒ (√x)⁴ = 0.25

⇒ x² = 0.25 = (0.5)²

∴ x = 0.5

Ex 12.(ii) log₁₀ (7x-5) = 2 হলে, x -এর মান

(a) 10   (b) 12   (c) 15  (d) 18

সঠিক উত্তরটি হলো (c) 15

সমাধান:

log₁₀ (7x-5) = 2

⇒ 7x-5 = 10²

⇒ 7x-5 = 100

⇒ 7x = 105

⇒ x = 105/7 = 15

∴ x = 15

Ex 12.(iii) log₂3 = a হলে, log₈27 হবে

(a) 3a   (b) 1/a   (c) 2a  (d) a

সঠিক উত্তরটি হলো (d) a

সমাধান:

log ₈ 27 = log ₈ 3³

                = 3 log ₈ 3

               = 3/ (log₃ 8) [∵ log_ab=1/(log_ba)]

               = 3/ (log₃ 2³)

              = 3/ (3 log₃ 2)

              = 1/ (log₃ 2)

              = log₂ 3 = a (প্রদত্ত)

Ex 12.(iv) log_√2 x = a হলে, log_2√2 x হবে

(a) a/3   (b) a   (c) 2a  (d) 3a

সঠিক উত্তরটি হলো (a) a/3

সমাধান:

log_√2 x = a

⇒ x = (√2)^a 

∴ log_2√2 x = log_2√2(√2)^a

             = a log_2√2 √2

= a/ (log_√2 2√2) [∵ log_ab=1/(log_ba)]

= a/ (log_√2 (√2)³)

= a/ (3 log_√2 √2)

= a/3  [∵ log_a a=1 ]

Ex 12.(v) log _x 1/3 = -1/3 হলে, x-এর মান হবে

(a) 27   (b) 9   (c) 3  (d) 1/27

সঠিক উত্তরটি হলো (a) 27

সমাধান:

log _x 1/3 = -1/3

⇒ x^-1/3 = 1/3

⇒ (x^-1/3)³ = (1/3)³

⇒ x^-1 = 1/27

⇒ x^-1 = (27)^-1

∴ x = 27

Ex 13. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন:

Ex 13.(i) log₄log₄ log₄ 256-এর মান কত হবে হিসাব করি।

সমাধান:

log₄log₄ log₄ 256

= log₄log₄ log₄ 4⁴

= log₄log₄ 4 [∵ log_aa^k =k ]

= log₄1  [∵ log_aa =1 ]

= 0 [∵ log_a1 =0 ]

∴ log₄log₄ log₄ 256 -এর মান 0.

Ex 13.(ii) log (aⁿ/bⁿ) + log (bⁿ/cⁿ) +log(cⁿ/aⁿ) -এর মান কত হবে হিসাব করি।

সমাধান:

log (aⁿ/bⁿ) + log (bⁿ/cⁿ) +log(cⁿ/aⁿ)

= log aⁿ – log bⁿ +log bⁿ – log cⁿ + log cⁿ – log aⁿ     

= 0

∴ log (aⁿ/bⁿ) + log (bⁿ/cⁿ) +log(cⁿ/aⁿ) -এর মান 0.

Ex 13.(iii) দেখাই যে , a^log_ax = x

সমাধান:

ধরি, log_ax = z

⇒ a^z = x  …(i)

∴ a^log_ax = a^z , যেহেতু  z = log_ax

⇒ a^log_ax = x  [(i) থেকে পাই]

∴ a^log_ax = x   proved

Ex 13.(iv) log_e2  . log_x 25 = log ₁₀ 16 . log_e 10 হলে x -এর মান নির্ণয় করি।

সমাধান:

log_e2  . log_x 25 = log ₁₀ 16 . log_e 10

⇒ log_e2 . log_x 25  = log _e 16 [∵ log_am . log_an = log_a mn ] 

⇒ log_e2 . log_x 25 = log _e 2⁴

⇒ log_e2 . log_x 25 = 4log _e 2 [∵ k log_ab = log_a b^k ] 

⇒  log_x 25 = 4

⇒ x⁴ = 25 = (√5)⁴

∴ x = √5