WBBSE Class 9 সূচকের নিয়মাবলি koshe Dekhi 2 Solutions

Koshe Dekhi 2 Class 9 | কষে দেখি 2 ক্লাস 9 | Class 9 Laws of Indices Koshe Dekhi 2 Solutions | গণিত প্রকাশ ক্লাস ৯ সূচকের নিয়মাবলি কষে দেখি ২ সমাধান | WBBSE Class 9 Laws of Indices Chapter 7 Solution | সূচকের নিয়মাবলি কষে দেখি ২ সমাধান  | Ganit Prakash Class 9 Solution Koshe Dekhi 2 | Solution of WB Board Class 9 Laws of Indices Exercise 2 |  গণিত প্রকাশ নবম শ্রেণি কষে দেখি ২ সমাধান

WBBSE Math Koshe Dekhi 2 Class 9 Solutions | গণিত প্রকাশ নবম শ্রেণি কষে দেখি ২ সমাধান

ক্লাস ৯ সূচকের নিয়মাবলি কষে দেখি ২ Question 1 সমাধান

Ex 1. মান নির্ণয় করি

গণিত প্রকাশ ক্লাস ৯ সূচকের নিয়মাবলি কষে দেখি ২ Question 2 সমাধান

Ex 2. সরল করি

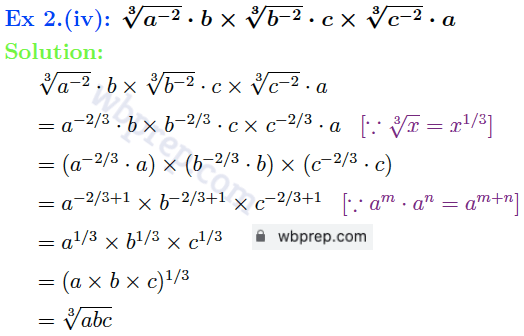
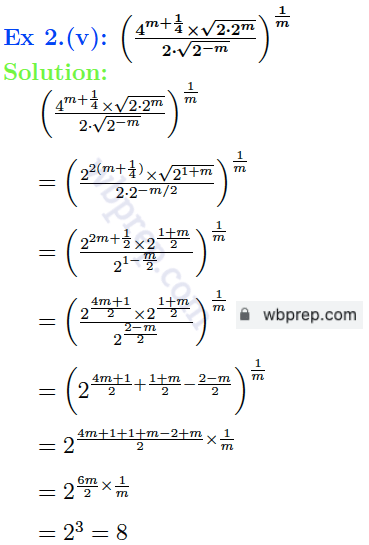
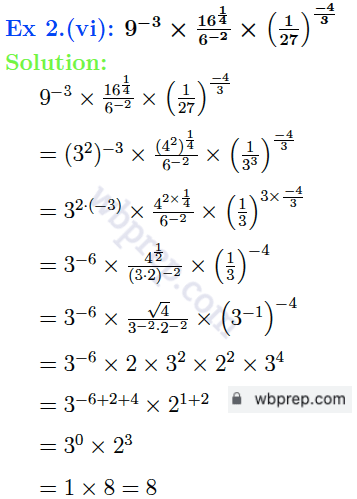
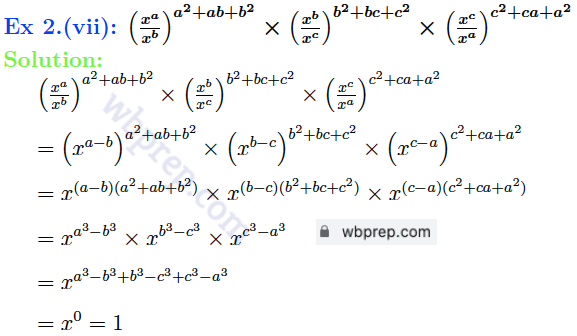
WBBSE Class 9 Laws of Indices Question 3 Solution:

ক্লাস ৯ কষে দেখি ২ Question 4 সমাধান

Ex 4: প্রমাণ করি:

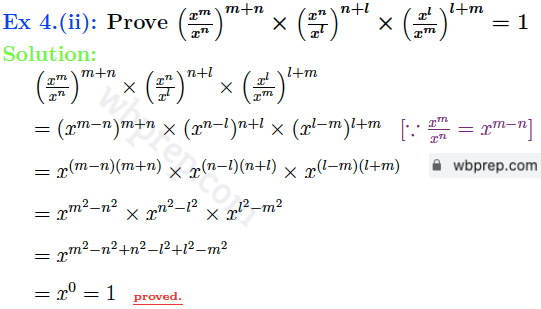
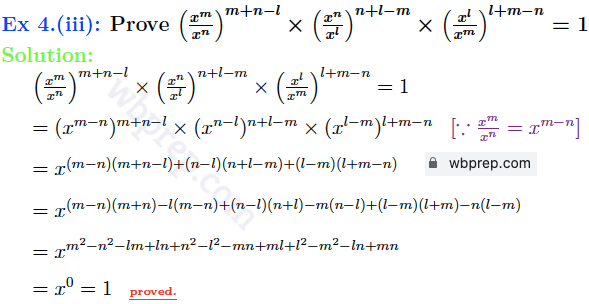
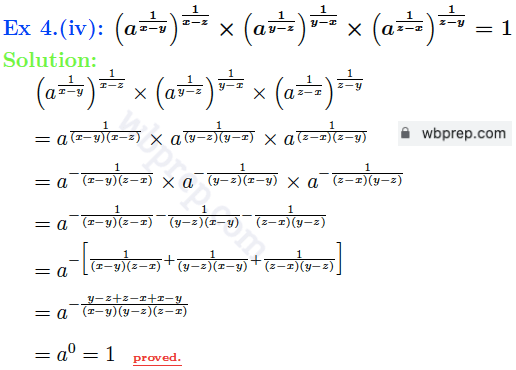
WBBSE Class 9 Laws of Indices Question 5 Solution:

Ex 5. x+z=2y এবং b²=ac হলে দেখাই যে a^y-z b^z-x c^x-y =1

সমাধান:

 x+z = 2y      ⇒ x-y = y-z

এখন, a^y-z b^z-x c^x-y

= a^y-z b^z-x c^y-z  [∵ x-y = y-z]

= (ac)^y-z b^z-x

= (b²)^y-z b^z-x  [∵ ac=b²]

= b^2y-2z b^z-x

= b^2y-2z+z-x

= b^2y-(x+z)

= b^2y-2y [∵ x+z = 2y]

= b⁰

=1  proved

WBBSE Class 9 Laws of Indices Question 6 Solution:

Ex 6. a=xy ^p-1 , b=xy^q-1 এবং c=xy^r-1 হলে দেখাই যে, a^q-r b^r-p  c^p-q =1

সমাধান:

a^q-r b^r-p  c^p-q

= (xy^p-1)^q-r (xy^q-1)^r-p (xy^r-1)^p-q

= x^q-r y^(p-1)(q-r) x^r-p y^(q-1)(r-p) x^p-q y^(r-1)(p-q)

= x^q-r+r-p+p-q  y^{(p-1)(q-r)+(q-1)(r-p)+(r-1)(p-q)}

= x⁰ y^{(pq-q-pr+r +qr-r-pq+p+pr-p-qr+q)}

= x⁰ y⁰

= 1    proved

Ex 7. $x^\frac{1}{a}=y^\frac{1}{b}=z^\frac{1}{c}$ এবং xyz=1 হলে, দেখাও যে, a+b+c=0.

সমাধান:

ধরি, $x^\frac{1}{a}=y^\frac{1}{b}=z^\frac{1}{c}=k,$ যেখানে k(≠0) একটি ধ্রুবক ।

∴ $x^\frac{1}{a}=k$ ⇒ x=k^a

$y^\frac{1}{b}=k$ ⇒ y=k^b

$z^\frac{1}{c}=k$ ⇒ z=k^c

এখন, xyz =1

⇒ k^a⋅k^b⋅k^c = 1

⇒ k^a+b+c = k⁰

⇒ a+b+c =0 প্রমাণিত

Ex 8. a^x = b^y = c^z এবং abc=1 হলে, দেখাও যে, xy+yz+zx=0

সমাধান:

ধরি, a^x = b^y = c^z =k, যেখানে k(≠0) একটি ধ্রুবক ।

∴ a=k^1/x, b=k^1/y, c=k^1/z

এখন, abc =1

⇒ k^1/x⋅k^1/y⋅k^1/z = 1

⇒ $k^{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}$ = k⁰

⇒ $k^{\frac{yz+zx+xy}{xyz}}$ = k⁰

⇒ $\dfrac{yz+zx+xy}{xyz}$ = k⁰

⇒ xy+yz+zx =0 প্রমাণিত

Ex 9. সমাধান করি:

Ex 9.(i) 49^x= 7³

সমাধান:

49^x = 7³

⇒ (7²)^x = 7³

⇒ 7^2x = 7³

⇒ 2x =3

⇒ x = 3/2

Ex 9.(ii) 2^x+2+ 2^x-1 = 9

সমাধান:

2^x+2+ 2^x-1 = 9

⇒ 2^x . 2² + 2^x. 2^-1 =9

⇒ 2^x. 4 + 2^x . (1/2) =9

⇒ 2^x (4+ 1/2)= 9

⇒ 2^x (9/2) = 9

⇒ 2^x =9 × 2/9

⇒ 2^x = 2= 2¹ 

⇒ x = 1 

Ex 9.(iii) 2^x+1 + 2^x+2 =48

সমাধান:

2^x+1 + 2^x+2 =48

⇒ 2^x . 2¹ +2^x . 2² =48

⇒ 2^x . 2+2^x . 4=48

⇒ 2^x(2+4) =48

⇒ 2^x × 6 =48

⇒ 2^x = 8 = 2³

⇒ x = 3 

Ex 9.(v) 9× 81^x = 27^2-x

সমাধান:

9× 81^x = 27^2-x

⇒ 3² × 3^4x = 3^3(2-x)

⇒ 3^2+4x = 3^6-3x

⇒ 2+4x = 6-3x

⇒ 4x+3x = 6-2

⇒ 7x = 4

⇒ x = 4/7 

Ex 9.(vi) 2^5x+4 +2⁹=2¹⁰

সমাধান:

2^5x+4 +2⁹=2¹⁰

⇒ 2^5x+4 =2¹⁰ -2⁹

⇒ 2^5x+4 =2⁹(2-1)

⇒ 2^5x+4 = 2⁹

⇒ 5x+4 =9

⇒ 5x =9-4

⇒ 5x=5

⇒ x = 5/5 =1

∴ x = 1 

Ex 9.(vii) 6^2x+4 = 3^3x  . 2^x+8

সমাধান:

6^2x+4 = 3^3x  . 2^x+8

⇒ (3×2)^2x+4 = 3^3x . 2^x+8

⇒ 3^2x+4 . 2^2x+4 = 3^3x . 2^x+8

⇒ $\dfrac{2^{2x+4}}{2^{x+8}} = \dfrac{3^{3x}}{3^{2x+4}}$

⇒  2^2x+4-x-8 = 3^3x-2x-4

⇒ 2^x-4 = 3^x-4

⇒ (2/3)^x-4 = 1 = (2/3)⁰

⇒ x-4 =0

⇒ x = 4

Ex 10. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)

Ex 10.(i) (0.243)^0.2 ✕ (10)^0.6 এর মান

(a) 0.3   (b) 3   (c) 0.9  (d) 9

সঠিক উত্তরটি হলো (b) 3

সমাধান:

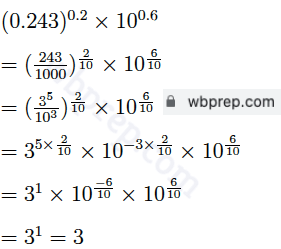
Ex 10.(ii) 2^1/2 × 2 ^-1/2 × (16)^1/2 এর মান

(a) 1   (b) 2   (c) 4  (d) 1/2

সঠিক উত্তরটি হলো (c) 4

সমাধান:

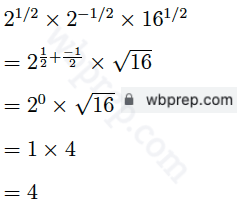
Ex 10.(iii) 4^x = 8³ হলে x এর মান 

(a) 3/2   (b) 9/2   (c) 3  (d) 9

সঠিক উত্তরটি হলো (b) 9/2

সমাধান:

4^x = 8³

⇒ (2²)^x = (2³)³

⇒ 2^2x = 2⁹

⇒ 2x= 9 

∴ x = 9/2

Ex 10.(iv)  20^–x = 1/7 হলে (20)^2x এর মান

(a) 1/49   (b) 7   (c) 49  (d) 1

সঠিক উত্তরটি হলো (c) 49

সমাধান:

20^–x = 1/7

⇒ 20^–x = 7^-1

⇒ 20^x = 7¹ = 7

⇒ (20)^2x = 7² = 49

Ex 10.(v)  4 × 5^x = 500 হলে x^x এর মান

(a) 8   (b) 1   (c) 64  (d) 27

সঠিক উত্তরটি হলো (d) 27

সমাধান:

4 × 5^x = 500

⇒ 5^x = 500/4

⇒ 5^x = 125

⇒ 5^x = 5³

⇒ x = 3

∴ x^x = 3³ = 27

Ex 11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন:

Ex 11.(i) (27)^x =(81)^y  হলে x : y কত হয় লিখি।

সমাধান:

(27)^x = (81)^y

⇒ (3³)^x = (3⁴)^y

⇒ 3^3x = 3^4y

⇒ 3x=4y

⇒ x/y = 4/3

⇒ x:y = 4:3

Ex 11.(ii) (5⁵ + 0.01)² –(5⁵ -0.01)² = 5^x হলে x এর মান কত হিসাব করে লিখি।

সমাধান:

(5⁵ + 0.01)² –(5⁵ – 0.01)² = 5^x

⇒ 4 × 5⁵ × 0.01 = 5^x [∵ (a+b)²-(a-b)²=4ab ]

⇒ 0.04 × 5⁵ = 5^x

⇒ 4/100 = 5^x-5

⇒ 1/25  = 5^x-5

⇒ 5^-2 = 5^x-5

⇒  x-5 = -2

⇒ x = 5-2 = 3

∴ x = 3

Ex 11.(iii) 3× 27^x = 9^x+4 হলে x এর মান কত হিসাব করে লিখি।

সমাধান:

3 × 27^x = 9^x+4

⇒ 3 × 3^3x = 3^2(x+4) 

⇒ 3^1+3x = 3^2x+8

⇒ 1+3x = 2x+8

⇒ 3x-2x = 8-1

⇒ x=7

∴ x = 7

Ex 11.(iv) $\sqrt[3]{(\frac{1}{64})^{\frac{1}{2}}}$ এর মান কত হিসাব করে লিখি।

সমাধান: